Édit du 17/08/2024 : ajout de la version belge
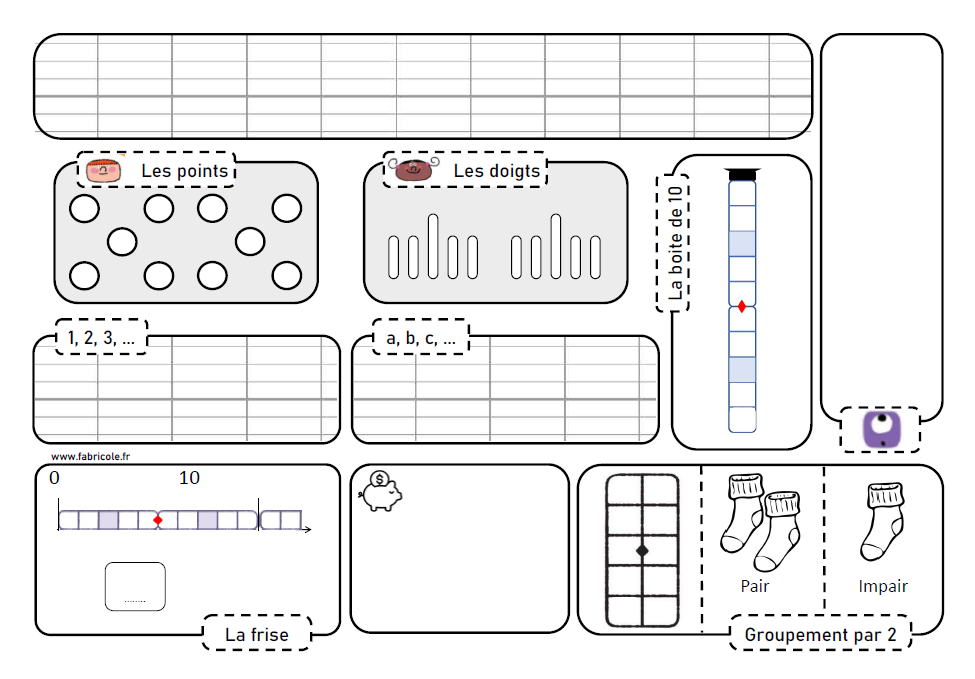
Outre les différentes représentations du nombre, ce rituel permet d’aborder progressivement tout au long de l’année : les nombres ordinaux, l’écriture des nombres en chiffres et en lettres, la notion de centaine, dizaine et unité, la frise numérique, la monnaie, la notion de parité, les décompositions, le tableau des nombres, l’ajout et le retrait d’unités et de dizaines entières, le complément à la dizaine supérieure, …
Bien sûr, ce rituel avance plus vite que la méthode des Noums. Ce n’est pas grave et même au contraire, il prépare les notions qui seront revues plus en détail ensuite au cours des séances.
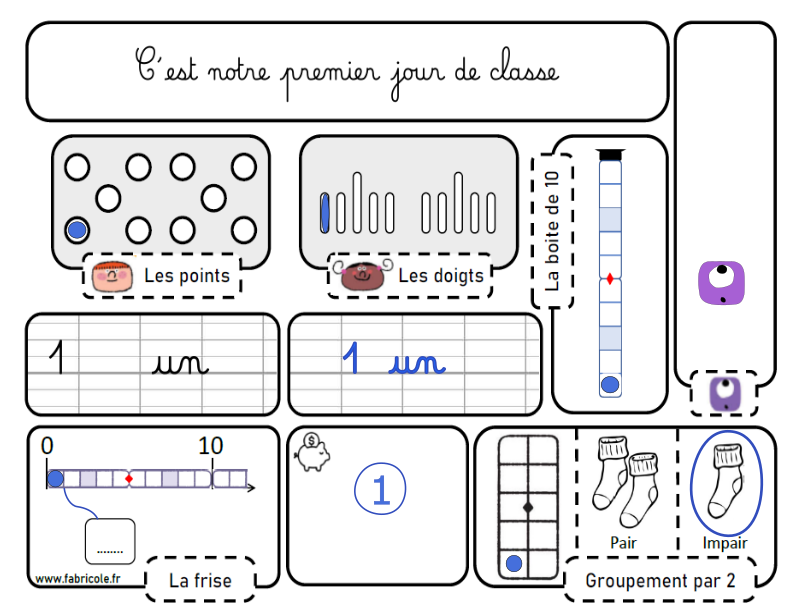
Un rituel progressif : les 10 premiers jours
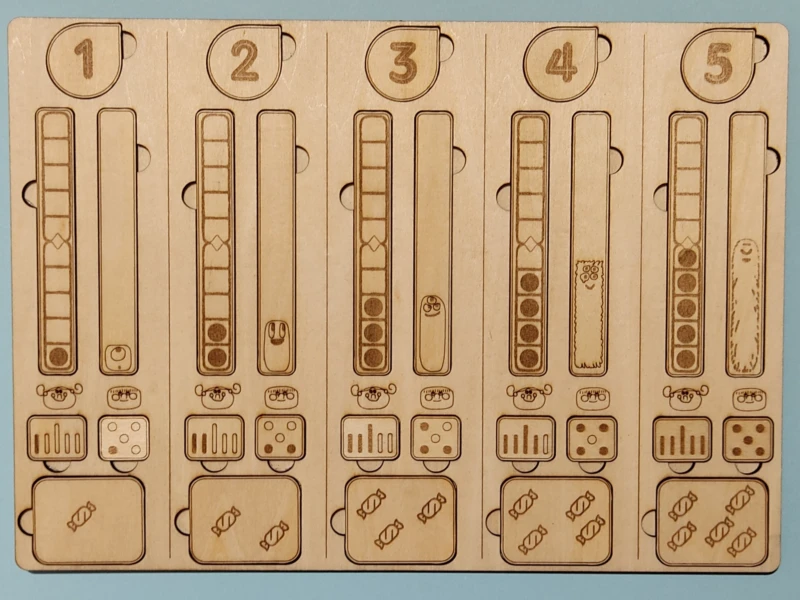
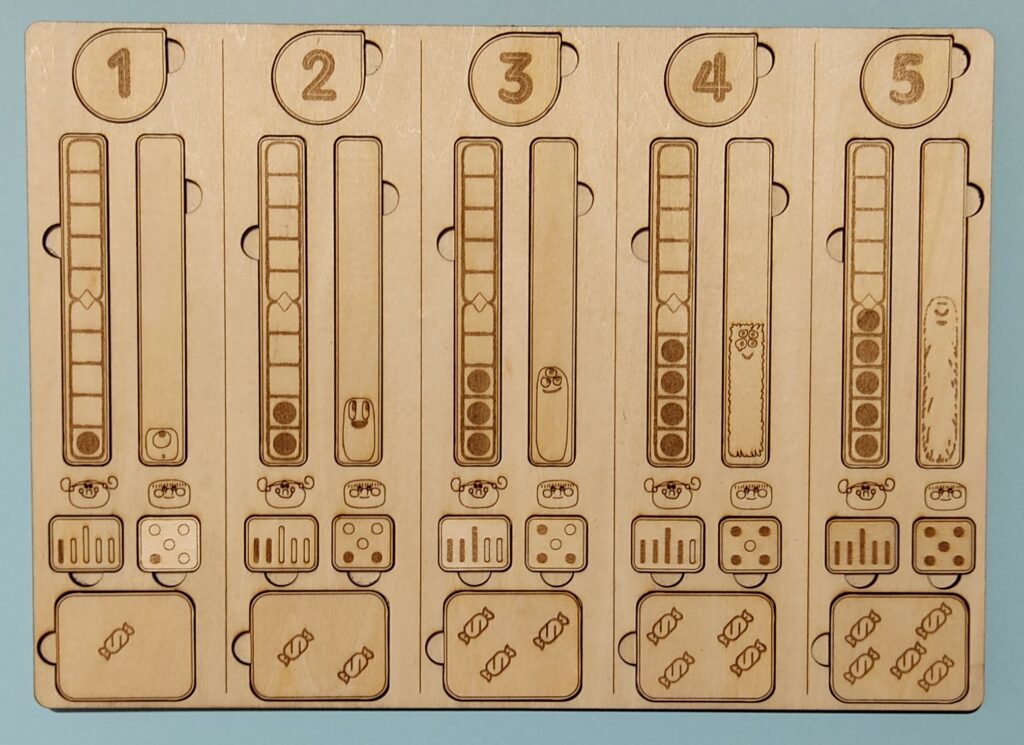
Pour les 10 premiers jours, le rituel comporte essentiellement les différentes représentations du nombre utilisées dans la méthode des Noums. Il s’agit de colorier les points et les doigts, recopier le nombre en chiffre et en lettres, mettre le bon nombre de jetons dans la boite de 10, coller le noum correspondant, mettre le bon nombre de jeton dans la boite de la frise numérique et relier à la frise, dessiner les pièces et les billets nécessaires pour atteindre le montant recherché (avec le moins de pièces et de billets possibles), mettre le bon nombre de jetons dans la boite de groupement par 2 et indiquer si le nombre est pair ou impair (en entourant ou en coloriant)
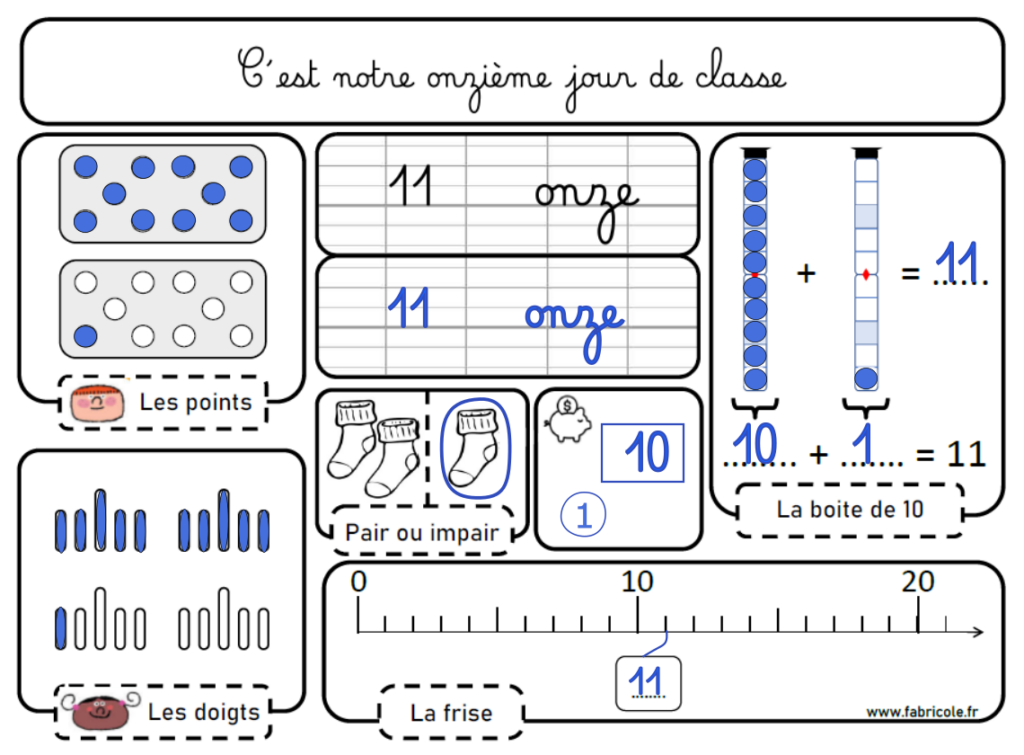
Du jour 11 au jour 20 :
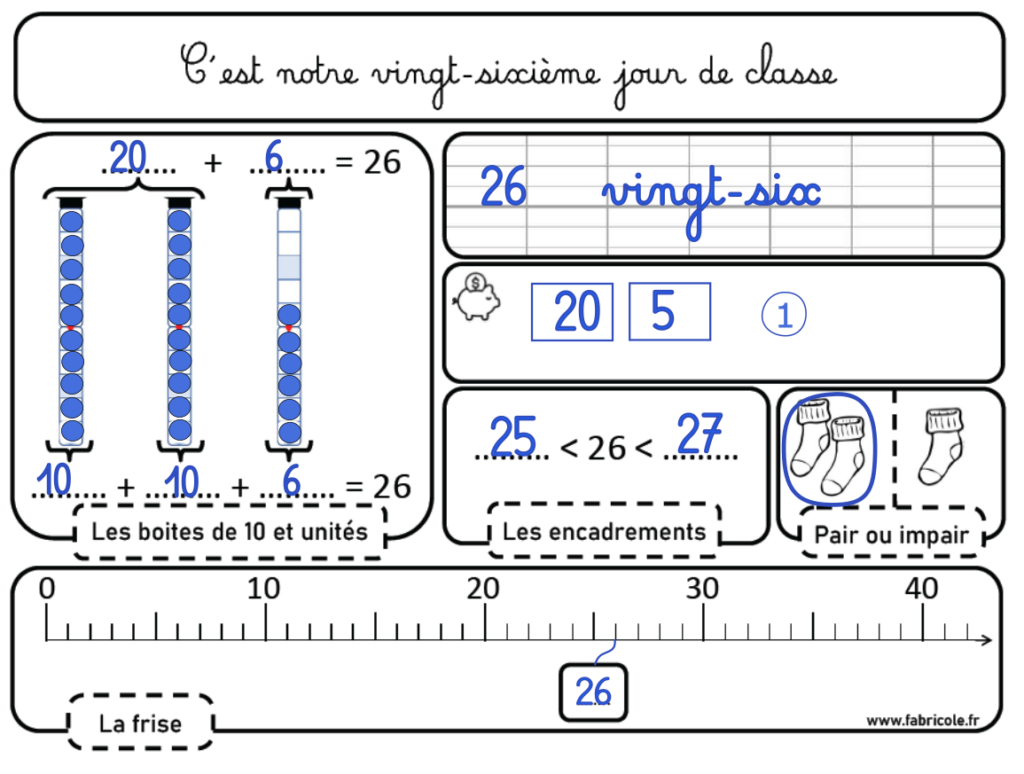
Pour les jours 11 à 20, on introduit la notion de décomposition en dizaines et unités en douceur grâce aux jetons dans les boites de 10. La frise numérique est modifiée en frise classique, sans notion de « boite »
Du jour 21 au jour 30 :
A partir du 21e jour, on complète la notion de décomposition, toujours en appui des boites de 10. 24 c’est 20+4 mais c’est aussi 10+10+4 et on introduit le nombre d’avant et le nombre d’après avec au passage, une brève explication du signe <.
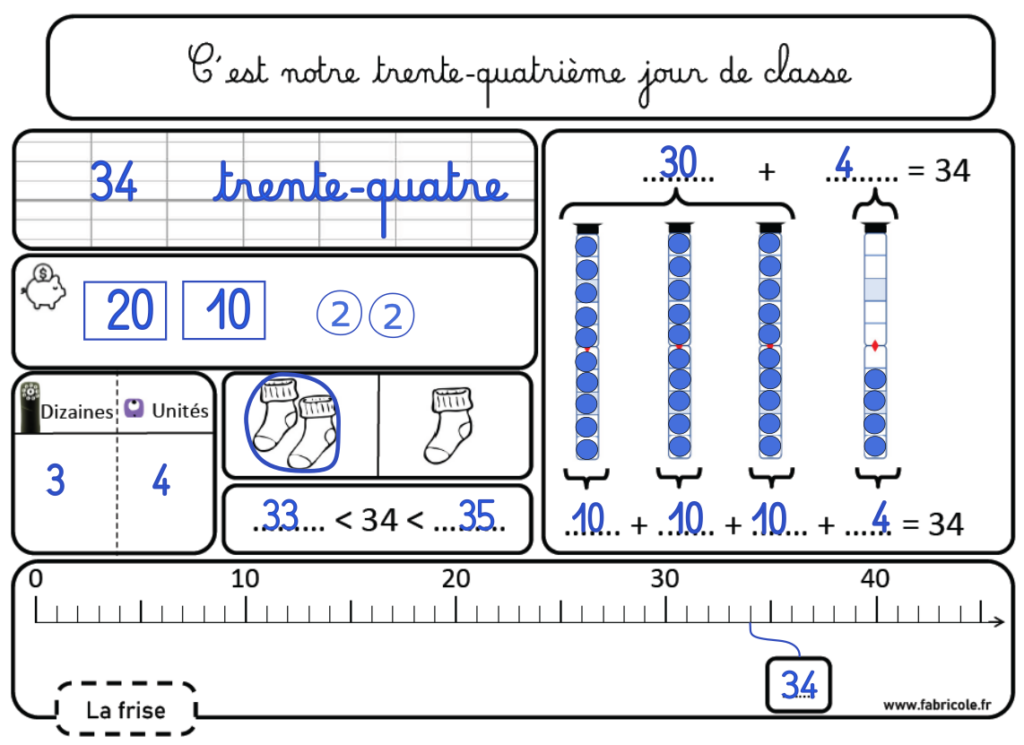
Du jour 31 au jour 40 :
Au 31e jour, on décompose toujours le nombre mais on indique dans un tableau le nombre de noums 10 et le nombre de noums 1
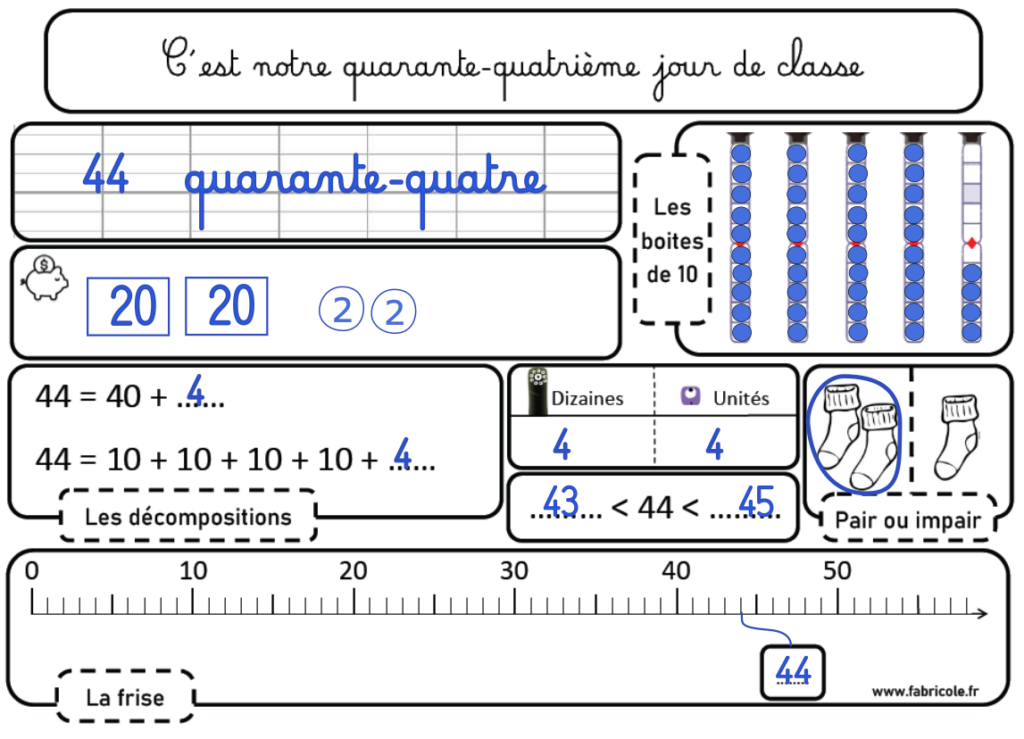
Du jour 41 au jour 50 :
Les décompositions sont détachées des boites de 10 pour que l’élève apprenne à s’en passer.
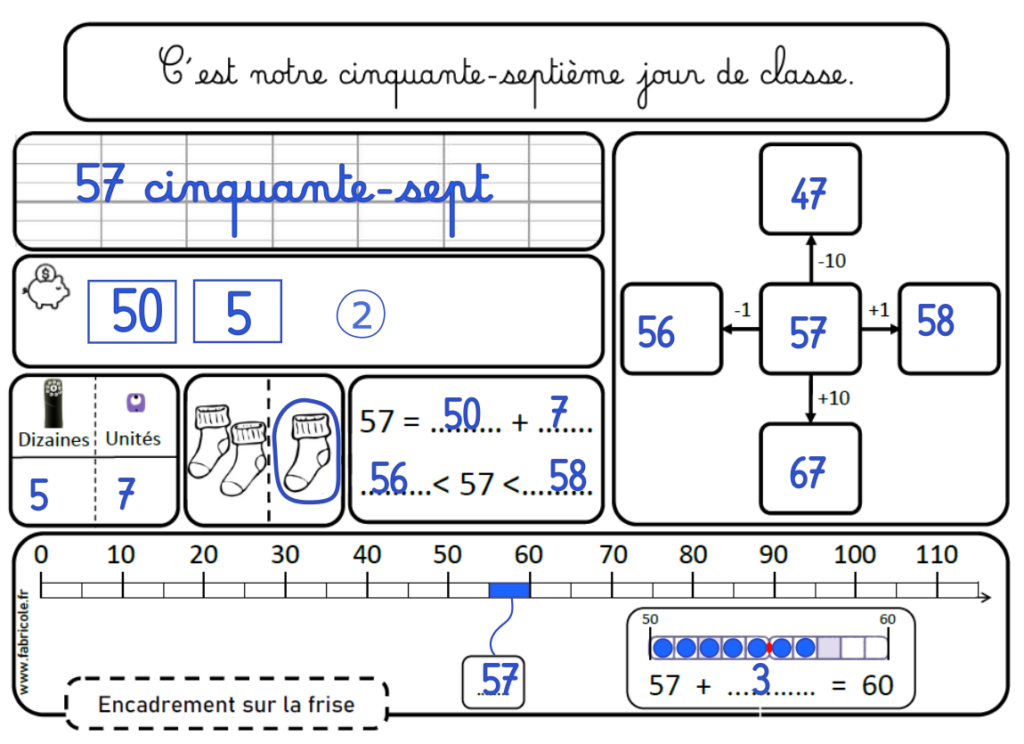
A partir du jour 51 :
Pour les nombres après 50, les boites de 10 disparaissent pour laisser la place au tableau des nombres et l’ajout et le retrait d’une unité et d’une dizaine.
La frise numérique est modifiée pour laisser place à un travail sur les encadrements. Par exemple, pour le 56e jour, l’élève doit trouver la case correspondant à l’encadrement de 56 et donc colorier la case entre 55 et 60. Pour l’aider dans cette tâche, il complète l’agrandissement de la frise entre 50 et 60 et s’appuie sur les repères disponibles : le début de la boite, la fin de la boite, le losange et sur la frise, le repère du 50, celui du 60 et le petit trait du 55.
Enfin, il complète le calcul du complément à la dizaine supérieure en appui avec la boite de 10 et relie la carte du nombre à son emplacement approximatif sur la frise. Toujours avec notre exemple du nombre 56, on relie la carte à un emplacement juste après le trait du 55 puisque 56 c’est juste 1 de plus que 55.
Comment l’utiliser ?
Personnellement, mes élèves réalisent ce rituel pendant le temps d’accueil puis un élève vient « jouer à la maitresse » pour corriger en collectif dans la foulée.
Quand il y a une nouveauté, ils font ce qu’ils savent faire et je me charge de la correction pour expliquer la nouveauté.
J’imprime les fiches en paramétrant 2 pages sur un A4. Cette fiche est ensuite collée dans le cahier du jour quand l’élève a fini son atelier d’écriture.
Pour me suivre :
Sur Twitter : @fabricole59
Sur Facebook : Fabricole59
Sur Instagram : fabricole59
Pour participer aux réflexions sur le FabLab à l’école, rejoignez-moi sur le groupe Facebook : FabLab à l’école
Pour télécharger le document :
Document utilisable en classe à condition de ne pas le modifier et de laisser la source visible.
Version française :
Version belge :